Nash Equilibrium represents a strategy profile where no player can benefit by unilaterally changing their strategy, while Subgame Perfect Equilibrium refines this concept by requiring strategies to constitute a Nash Equilibrium in every subgame, ensuring credibility in dynamic games. Explore the key differences and applications of these equilibrium concepts in this article.
Table of Comparison
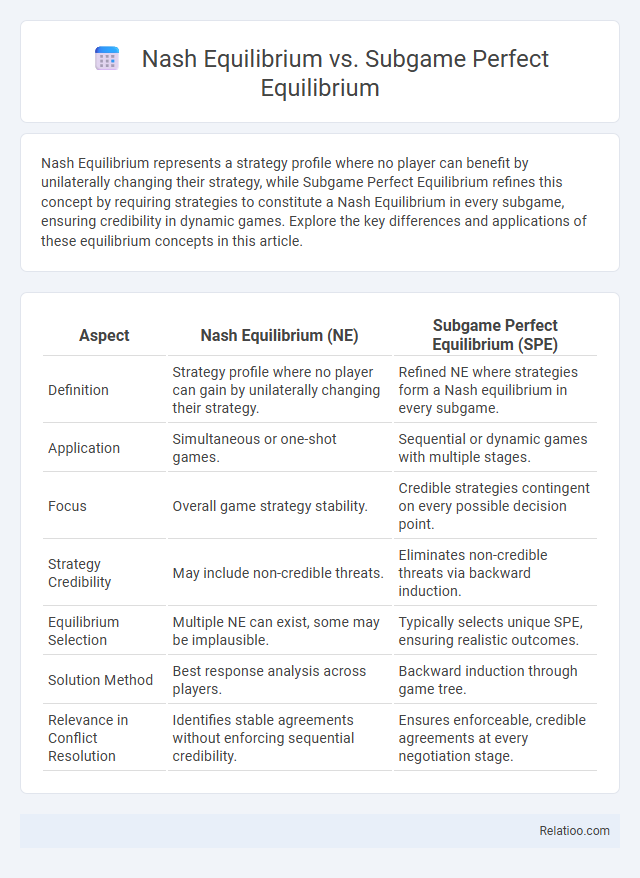
| Aspect | Nash Equilibrium (NE) | Subgame Perfect Equilibrium (SPE) |
|---|---|---|
| Definition | Strategy profile where no player can gain by unilaterally changing their strategy. | Refined NE where strategies form a Nash equilibrium in every subgame. |
| Application | Simultaneous or one-shot games. | Sequential or dynamic games with multiple stages. |
| Focus | Overall game strategy stability. | Credible strategies contingent on every possible decision point. |
| Strategy Credibility | May include non-credible threats. | Eliminates non-credible threats via backward induction. |
| Equilibrium Selection | Multiple NE can exist, some may be implausible. | Typically selects unique SPE, ensuring realistic outcomes. |
| Solution Method | Best response analysis across players. | Backward induction through game tree. |
| Relevance in Conflict Resolution | Identifies stable agreements without enforcing sequential credibility. | Ensures enforceable, credible agreements at every negotiation stage. |
Introduction to Game Theory Concepts
Nash Equilibrium represents a strategy profile where no player can benefit by unilaterally changing their strategy, ensuring stability in simultaneous-move games. Subgame Perfect Equilibrium refines this concept by requiring players' strategies to constitute a Nash Equilibrium in every subgame, addressing dynamic games with sequential moves. Understanding these equilibrium concepts helps you analyze strategic interactions and predict outcomes in game theory with greater precision.
Defining Nash Equilibrium
Nash Equilibrium occurs when no player can benefit by unilaterally changing their strategy, given the strategies of all other players. Subgame Perfect Equilibrium refines this concept by requiring that strategies constitute a Nash Equilibrium in every subgame, ensuring credibility in sequential games. Understanding your specific game context helps determine which equilibrium concept best predicts rational player behavior.
Understanding Subgame Perfect Equilibrium
Subgame Perfect Equilibrium refines the concept of Nash Equilibrium by requiring that strategies form a Nash Equilibrium in every subgame, ensuring credibility and consistency of decisions at every stage. This equilibrium concept eliminates non-credible threats and promises, which can occur in Nash Equilibria when players consider future moves. Understanding Subgame Perfect Equilibrium helps You analyze dynamic games where sequential moves and strategic foresight are critical, identifying stable and rational outcomes throughout the entire game tree.
Key Differences Between Nash and Subgame Perfect Equilibrium
Nash Equilibrium represents a strategy profile where no player can benefit by unilaterally changing their action, assuming other players' strategies remain fixed, but it does not require credibility of each player's threat or promise in every part of the game. Subgame Perfect Equilibrium refines this concept by demanding that strategies constitute a Nash Equilibrium in every subgame, ensuring credibility and consistency throughout the entire game tree. You should focus on how Subgame Perfect Equilibrium eliminates non-credible threats found in some Nash Equilibria, making it a stronger and more precise solution concept in dynamic or sequential games.
Applications of Nash Equilibrium in Strategic Decision-Making
Nash Equilibrium identifies stable strategy profiles where no player benefits from unilaterally changing their choice, crucial in competitive markets and auction designs. Subgame Perfect Equilibrium enhances this by ensuring credible strategies in every subgame, used extensively in sequential decision-making and bargaining scenarios. Your strategic decisions leverage Nash Equilibrium to predict rivals' behavior, optimize outcomes in oligopoly pricing, and design contracts that anticipate competitor responses.
Real-World Examples of Subgame Perfect Equilibrium
Subgame Perfect Equilibrium (SPE) refines the Nash Equilibrium by requiring strategies to be optimal at every point in a dynamic game, ensuring credibility in sequential decision-making. Real-world examples of SPE include bargaining scenarios where each party anticipates future responses, such as in negotiating labor contracts or international trade agreements. You can observe SPE in situations like the sequential entry of firms into a market, where each firm's decision is contingent on prior moves, ensuring strategic consistency throughout the game.
Solving Games: Nash vs Subgame Perfect Approaches
Nash Equilibrium identifies strategy profiles where no player can benefit from unilaterally changing their choice, applicable in simultaneous-move games. Subgame Perfect Equilibrium refines this concept by requiring strategy profiles to represent Nash Equilibria in every subgame, ensuring credible threats and promises in sequential games. Your decision-making improves by selecting Subgame Perfect Equilibrium for dynamic games, while Nash Equilibrium suits static game analysis.
Limitations of Nash and Subgame Perfect Equilibrium
Nash Equilibrium often assumes players choose strategies simultaneously without accounting for dynamic game structures, which can lead to unrealistic predictions in sequential games. Subgame Perfect Equilibrium refines Nash by requiring strategy credibility at every subgame, but it still struggles with complexity in extensive-form games and may not capture behavioral irrationalities or incomplete information. Your strategic analysis benefits from recognizing these limitations, as neither equilibrium concept fully addresses real-world scenarios involving imperfect commitment and bounded rationality.
Importance in Economic and Social Contexts
Nash Equilibrium represents a stable state where no player can benefit from unilaterally changing their strategy, crucial for predicting outcomes in competitive markets and social interactions. Subgame Perfect Equilibrium refines this concept by ensuring strategy credibility within every possible decision point, making it vital for analyzing dynamic games such as negotiations and political strategies. Understanding these equilibrium concepts empowers your ability to anticipate behavior in economic models and social systems, guiding optimal decision-making in strategic environments.
Conclusion: Choosing the Right Equilibrium Solution
Choosing the right equilibrium solution depends on the complexity and structure of your strategic interaction. Nash Equilibrium provides a stable outcome where no player can benefit by unilaterally changing their strategy, whereas Subgame Perfect Equilibrium refines this concept by ensuring credibility and optimality in every subgame, making it ideal for sequential decisions. Your choice should align with whether the game involves simultaneous moves or a dynamic sequence of actions to ensure accurate and practical predictions.
Infographic: Nash Equilibrium vs Subgame Perfect Equilibrium
 relatioo.com
relatioo.com