Correlated Equilibrium extends Nash Equilibrium by allowing players to coordinate their strategies through shared signals, potentially leading to higher collective payoffs. Explore how these equilibrium concepts differ and impact strategic decision-making in this article.
Table of Comparison
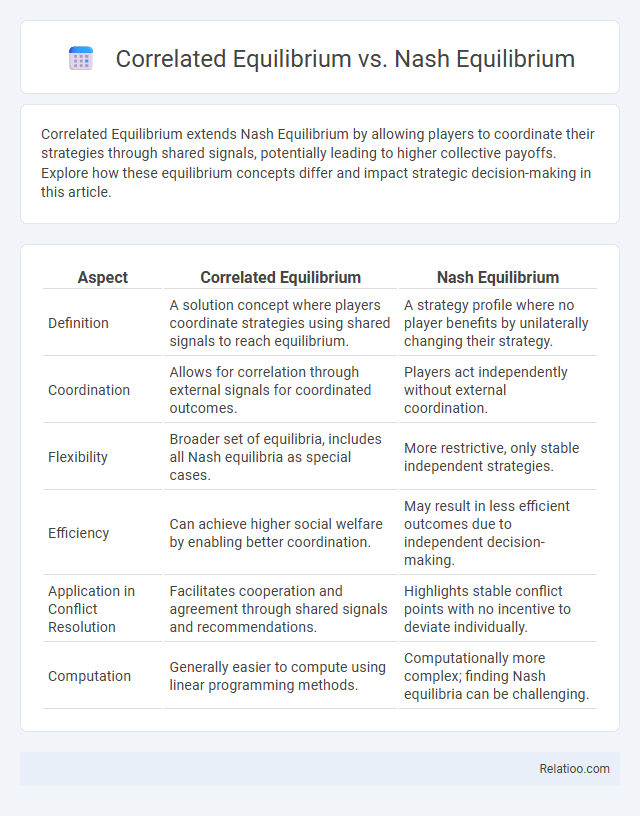
| Aspect | Correlated Equilibrium | Nash Equilibrium |
|---|---|---|
| Definition | A solution concept where players coordinate strategies using shared signals to reach equilibrium. | A strategy profile where no player benefits by unilaterally changing their strategy. |
| Coordination | Allows for correlation through external signals for coordinated outcomes. | Players act independently without external coordination. |
| Flexibility | Broader set of equilibria, includes all Nash equilibria as special cases. | More restrictive, only stable independent strategies. |
| Efficiency | Can achieve higher social welfare by enabling better coordination. | May result in less efficient outcomes due to independent decision-making. |
| Application in Conflict Resolution | Facilitates cooperation and agreement through shared signals and recommendations. | Highlights stable conflict points with no incentive to deviate individually. |
| Computation | Generally easier to compute using linear programming methods. | Computationally more complex; finding Nash equilibria can be challenging. |
Introduction to Equilibrium Concepts in Game Theory
Equilibrium concepts in game theory provide frameworks to predict players' strategies in strategic interactions, with Nash Equilibrium representing a state where no player benefits from unilaterally changing their strategy. Correlated Equilibrium extends this by allowing players to coordinate strategies based on signals from an external correlation device, potentially achieving higher joint payoffs than Nash Equilibria. The general term Equilibrium encompasses various solution concepts that capture stable strategy profiles where players' expectations and actions align according to specific rationality assumptions.
Defining Nash Equilibrium
Nash Equilibrium refers to a strategic scenario where no player can gain by unilaterally changing their strategy given the strategies of others, representing stability in non-cooperative games. Correlated Equilibrium generalizes this concept by allowing players to coordinate their strategies through signals, potentially yielding higher payoffs. Understanding Nash Equilibrium helps you analyze how rational players interact without external coordination, distinguishing it from broader equilibrium concepts in game theory.
Understanding Correlated Equilibrium
Correlated Equilibrium extends the concept of Nash Equilibrium by allowing players to coordinate their strategies through a public signal, enabling correlated strategies that can lead to higher payoffs overall. Unlike Nash Equilibrium, where each player independently chooses a best response to others' strategies, Correlated Equilibrium leverages shared signals to produce outcomes that are stable and mutually beneficial. Understanding Correlated Equilibrium deepens your insight into strategic decision-making by highlighting how external coordination can improve individual and collective payoffs beyond standard equilibrium concepts.
Key Differences Between Nash and Correlated Equilibria
Nash equilibrium occurs when each player's strategy is optimal given the strategies of others, with no player benefiting from unilaterally changing their own action. Correlated equilibrium extends this by allowing players to coordinate their strategies based on shared signals, potentially leading to higher overall payoffs than Nash equilibria. Your choice between these concepts depends on whether strategy coordination is feasible, with correlated equilibria representing a broader and potentially more efficient solution concept in game theory.
Mathematical Formulations and Examples
Correlated Equilibrium extends Nash Equilibrium by allowing players to coordinate strategies based on signals from a public random source, mathematically represented by joint probability distributions over strategy profiles satisfying incentive constraints. Nash Equilibrium is defined by a strategy profile where no player can improve their payoff by unilaterally deviating, expressed as a fixed point in best response functions. Your understanding of equilibrium concepts deepens by comparing examples such as the Prisoner's Dilemma, where Nash Equilibrium results in mutual defection, whereas Correlated Equilibrium can lead to higher payoffs through correlated strategies.
Real-World Applications of Each Equilibrium
Correlated Equilibrium enables coordination in traffic signal timing, reducing congestion by allowing players to condition their strategies on shared signals, unlike Nash Equilibrium which models competitive market behaviors where each player independently optimizes their outcome. Nash Equilibrium finds real-world use in auctions and pricing strategies, where businesses assume rivals' actions remain fixed while optimizing their own decisions. General Equilibrium applies to entire economies, analyzing supply and demand across multiple markets simultaneously to predict how changes in policy or resources affect overall economic balance, providing You with comprehensive insights into interconnected market dynamics.
Strategic Advantages of Correlated Equilibrium
Correlated equilibrium offers strategic advantages over Nash equilibrium by allowing players to coordinate their strategies through external signals, leading to potentially higher payoffs and more efficient outcomes. Unlike Nash equilibrium, where players choose strategies independently, correlated equilibrium leverages shared information to reduce uncertainty and avoid suboptimal solutions. Your strategic decisions benefit from this coordination, enabling improved predictability and mutual gains in competitive environments.
Computational Complexity and Feasibility
Correlated Equilibrium (CE) offers computational advantages over Nash Equilibrium (NE) by allowing polynomial-time algorithms for finding solutions in many games, whereas computing NE is generally PPAD-complete and thus computationally intractable for large games. Equilibrium concepts differ in feasibility; CE requires a central signal or mediator to correlate players' strategies, making it more practical in environments that support communication, while NE assumes independent strategies without coordination. The broader category of Equilibrium encapsulates both CE and NE but varies widely in computational complexity depending on the equilibrium refinement and the game structure.
Limitations and Critiques of Both Concepts
Correlated Equilibrium often faces criticism for its reliance on an external correlation device, which may not be realistic in many strategic settings, making it less applicable in decentralized environments compared to Nash Equilibrium. Nash Equilibrium, while foundational, is limited by the assumption of perfect rationality and common knowledge among players, and it sometimes predicts multiple equilibria without clear selection criteria, reducing its predictive power. Both concepts struggle with computational complexity in large games and may fail to capture dynamic or evolving strategic interactions, restricting their practical usability in real-world applications.
Future Directions in Equilibrium Analysis
Future directions in equilibrium analysis emphasize expanding the applicability and computational efficiency of Correlated Equilibrium (CE) and Nash Equilibrium (NE) in complex strategic settings, including large-scale multi-agent systems and dynamic environments. Research explores algorithmic improvements leveraging machine learning to predict equilibrium behavior under uncertainty and incomplete information. Integrating CE's coordination advantages with NE's stability properties aims to enhance solution concepts for evolving economic, social, and technological networks.
Infographic: Correlated Equilibrium vs Nash Equilibrium
 relatioo.com
relatioo.com