FIR filters offer linear phase response and inherent stability, making them ideal for applications requiring precise phase control, while IIR filters provide efficient computation with fewer coefficients but may introduce phase distortions. Explore the key differences and applications of FIR and IIR filters to optimize your signal processing strategy in this article.
Table of Comparison
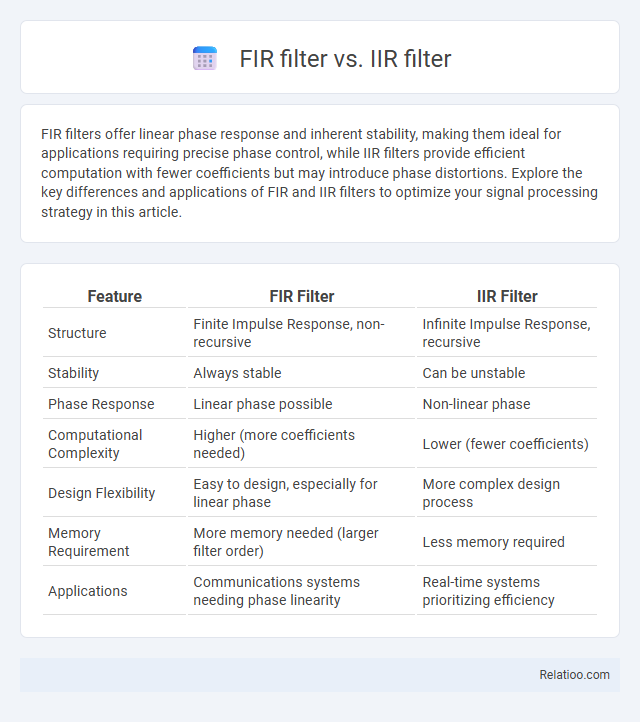
| Feature | FIR Filter | IIR Filter |
|---|---|---|
| Structure | Finite Impulse Response, non-recursive | Infinite Impulse Response, recursive |
| Stability | Always stable | Can be unstable |
| Phase Response | Linear phase possible | Non-linear phase |
| Computational Complexity | Higher (more coefficients needed) | Lower (fewer coefficients) |
| Design Flexibility | Easy to design, especially for linear phase | More complex design process |
| Memory Requirement | More memory needed (larger filter order) | Less memory required |
| Applications | Communications systems needing phase linearity | Real-time systems prioritizing efficiency |
Introduction to FIR and IIR Filters
FIR (Finite Impulse Response) filters have a finite duration of response to an impulse and are inherently stable with linear phase characteristics, making them ideal for applications requiring precise phase control. IIR (Infinite Impulse Response) filters feature feedback loops that produce an infinite-duration response, allowing more computational efficiency but with potential stability and phase distortion issues. Your choice between FIR and IIR filters depends on the specific requirements for stability, phase linearity, and computational complexity in your signal processing application.
Fundamental Differences Between FIR and IIR Filters
FIR filters have a finite impulse response due to their non-recursive structure, making them inherently stable and linear phase, whereas IIR filters use feedback, generating an infinite impulse response that allows for sharper frequency response with fewer coefficients. FIR filters require more computational resources for equivalent filter performance but provide exact linear phase characteristics, making them suitable for applications demanding phase linearity. IIR filters are more efficient in terms of computation and memory, yet their nonlinear phase response and potential instability require careful design and analysis.
Design Principles of FIR Filters
FIR filters are designed using a finite number of coefficients, ensuring inherent stability and linear phase response, which is critical for applications demanding minimal signal distortion. In contrast, IIR filters use feedback loops with infinite impulse responses, offering computational efficiency but potential stability challenges. FIR filter design principles emphasize windowing methods, frequency sampling, and optimization techniques like the Parks-McClellan algorithm to achieve precise amplitude and phase characteristics.
Design Principles of IIR Filters
IIR filters, unlike FIR filters, are designed using recursive algorithms that rely on feedback, enabling efficient realization with fewer coefficients for a given frequency response. The design principles of IIR filters focus on stability, causality, and meeting desired amplitude and phase specifications through pole-zero placement in the z-plane. When choosing between FIR and IIR filters, your design goals such as computational efficiency, phase linearity, and filter sharpness play a crucial role in selecting the appropriate filter type.
Frequency Response Comparison
FIR filters provide linear phase frequency response, ensuring no phase distortion, while IIR filters achieve sharper frequency response transitions with fewer coefficients but exhibit nonlinear phase characteristics. FIR filters are inherently stable due to their feedforward structure, whereas IIR filters may become unstable because of feedback loops despite efficient frequency selectivity. In comparison, general filter design choices depend on trade-offs between phase linearity, computational complexity, and frequency response sharpness tailored to specific signal processing applications.
Stability and Phase Characteristics
FIR filters exhibit inherent stability due to their non-recursive structure, ensuring a linear phase response ideal for applications requiring minimal phase distortion. IIR filters, while computationally efficient, can face stability challenges arising from their recursive feedback loops and typically display nonlinear phase characteristics. The choice between FIR and IIR filters depends on the balance between stability, phase linearity, and computational complexity required by the signal processing task.
Computational Complexity and Efficiency
FIR filters offer linear phase response and inherent stability, but they typically require higher computational complexity due to longer filter lengths and more multiplications per output sample compared to IIR filters. IIR filters achieve similar frequency responses with significantly fewer coefficients, resulting in lower computational load and higher efficiency, but they risk instability and nonlinear phase distortion. When selecting a filter for Your application, consider that FIR filters provide predictable performance with increased processing demands, while IIR filters deliver efficient computation at the potential cost of phase linearity and stability.
Applications of FIR Filters
FIR filters are widely used in applications requiring linear phase response and inherent stability, such as audio signal processing and data communications, where phase distortion must be minimized. Your choice of FIR filters ensures precise control over filter characteristics, making them ideal for multirate systems and adaptive filtering. Unlike IIR filters, FIR filters do not rely on feedback, which eliminates the risk of instability and makes them suitable for hardware implementation in real-time processing tasks.
Applications of IIR Filters
IIR filters are widely used in applications requiring efficient real-time signal processing due to their recursive structure and low computational cost. Your audio processing systems, telecommunications, and control systems benefit from IIR filters' ability to provide sharp frequency responses with fewer coefficients compared to FIR filters. Unlike FIR filters, which are preferred for linear phase requirements, IIR filters excel in scenarios where phase distortion is acceptable but minimal resource usage is critical.
Choosing the Right Filter for Your Project
Choosing the right filter for your project depends on factors like stability, phase response, and computational complexity. FIR filters offer linear phase response and guaranteed stability, making them ideal for applications requiring precise phase control. IIR filters provide efficient computation with fewer coefficients but can introduce nonlinear phase and potential stability issues, while general filters vary widely, necessitating careful analysis of project-specific requirements such as signal characteristics and resource constraints.
Infographic: FIR filter vs IIR filter
 relatioo.com
relatioo.com